Ph.D. in Computer Engineering, Data Scientist
Binary Classification
LearnDataSci is reader-supported. When you purchase through links on our site, earned commissions help support our team of writers, researchers, and designers at no extra cost to you.
What is Binary Classification?
In machine learning, binary classification is a supervised learning algorithm that categorizes new observations into one of two classes.
The following are a few binary classification applications, where the 0 and 1 columns are two possible classes for each observation:
| Application | Observation | 0 | 1 |
|---|---|---|---|
| Medical Diagnosis | Patient | Healthy | Diseased |
| Email Analysis | Not Spam | Spam | |
| Financial Data Analysis | Transaction | Not Fraud | Fraud |
| Marketing | Website visitor | Won't Buy | Will Buy |
| Image Classification | Image | Hotdog | Not Hotdog |
Quick example
In a medical diagnosis, a binary classifier for a specific disease could take a patient's symptoms as input features and predict whether the patient is healthy or has the disease. The possible outcomes of the diagnosis are positive and negative.
Evaluation of binary classifiers
If the model successfully predicts the patients as positive, this case is called True Positive (TP). If the model successfully predicts patients as negative, this is called True Negative (TN). The binary classifier may misdiagnose some patients as well. If a diseased patient is classified as healthy by a negative test result, this error is called False Negative (FN). Similarly, If a healthy patient is classified as diseased by a positive test result, this error is called False Positive(FP).
We can evaluate a binary classifier based on the following parameters:
- True Positive (TP): The patient is diseased and the model predicts "diseased"
- False Positive (FP): The patient is healthy but the model predicts "diseased"
- True Negative (TN): The patient is healthy and the model predicts "healthy"
- False Negative (FN): The patient is diseased and the model predicts "healthy"
After obtaining these values, we can compute the accuracy score of the binary classifier as follows: $$ accuracy = \frac {TP + TN}{TP+FP+TN+FN} $$
The following is a confusion matrix, which represents the above parameters:
In machine learning, many methods utilize binary classification. The most common are:
- Support Vector Machines
- Naive Bayes
- Nearest Neighbor
- Decision Trees
- Logistic Regression
- Neural Networks
The following Python example will demonstrate using binary classification in a logistic regression problem.
A Python example for binary classification
For our data, we will use the breast cancer dataset from scikit-learn. This dataset contains tumor observations and corresponding labels for whether the tumor was malignant or benign.
First, we'll import a few libraries and then load the data. When loading the data, we'll specify as_frame=True so we can work with pandas objects (see our pandas tutorial for an introduction).
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
dataset = load_breast_cancer(as_frame=True)
The dataset contains a DataFrame for the observation data and a Series for the target data.
Let's see what the first few rows of observations look like:
dataset['data'].head()| mean radius | mean texture | mean perimeter | mean area | mean smoothness | mean compactness | mean concavity | mean concave points | mean symmetry | mean fractal dimension | ... | worst radius | worst texture | worst perimeter | worst area | worst smoothness | worst compactness | worst concavity | worst concave points | worst symmetry | worst fractal dimension | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 17.99 | 10.38 | 122.80 | 1001.0 | 0.11840 | 0.27760 | 0.3001 | 0.14710 | 0.2419 | 0.07871 | ... | 25.38 | 17.33 | 184.60 | 2019.0 | 0.1622 | 0.6656 | 0.7119 | 0.2654 | 0.4601 | 0.11890 |
| 1 | 20.57 | 17.77 | 132.90 | 1326.0 | 0.08474 | 0.07864 | 0.0869 | 0.07017 | 0.1812 | 0.05667 | ... | 24.99 | 23.41 | 158.80 | 1956.0 | 0.1238 | 0.1866 | 0.2416 | 0.1860 | 0.2750 | 0.08902 |
| 2 | 19.69 | 21.25 | 130.00 | 1203.0 | 0.10960 | 0.15990 | 0.1974 | 0.12790 | 0.2069 | 0.05999 | ... | 23.57 | 25.53 | 152.50 | 1709.0 | 0.1444 | 0.4245 | 0.4504 | 0.2430 | 0.3613 | 0.08758 |
| 3 | 11.42 | 20.38 | 77.58 | 386.1 | 0.14250 | 0.28390 | 0.2414 | 0.10520 | 0.2597 | 0.09744 | ... | 14.91 | 26.50 | 98.87 | 567.7 | 0.2098 | 0.8663 | 0.6869 | 0.2575 | 0.6638 | 0.17300 |
| 4 | 20.29 | 14.34 | 135.10 | 1297.0 | 0.10030 | 0.13280 | 0.1980 | 0.10430 | 0.1809 | 0.05883 | ... | 22.54 | 16.67 | 152.20 | 1575.0 | 0.1374 | 0.2050 | 0.4000 | 0.1625 | 0.2364 | 0.07678 |
5 rows × 30 columns
The output shows five observations with a column for each feature we'll use to predict malignancy.
Now, for the targets:
dataset['target'].head()0 0
1 0
2 0
3 0
4 0
Name: target, dtype: int32The targets for the first five observations are all zero, meaning the tumors are benign. Here's how many malignant and benign tumors are in our dataset:
dataset['target'].value_counts()1 357
0 212
Name: target, dtype: int64So we have 357 malignant tumors, denoted as 1, and 212 benign, denoted as 0. So, we have a binary classification problem.
To perform binary classification using logistic regression with sklearn, we must accomplish the following steps.
Step 1: Define explanatory and target variables
We'll store the rows of observations in a variable X and the corresponding class of those observations (0 or 1) in a variable y.
X = dataset['data']
y = dataset['target']Step 2: Split the dataset into training and testing sets
We use 75% of data for training and 25% for testing. Setting random_state=0 will ensure your results are the same as ours.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y , test_size=0.25, random_state=0)Step 3: Normalize the data for numerical stability
Note that we normalize after splitting the data. It's good practice to apply any data transformations to training and testing data separately to prevent data leakage.
from sklearn.preprocessing import StandardScaler
ss_train = StandardScaler()
X_train = ss_train.fit_transform(X_train)
ss_test = StandardScaler()
X_test = ss_test.fit_transform(X_test)Step 4: Fit a logistic regression model to the training data
This step effectively trains the model to predict the targets from the data.
Step 5: Make predictions on the testing data
With the model trained, we now ask the model to predict targets based on the test data.
predictions = model.predict(X_test)Step 6: Calculate the accuracy score by comparing the actual values and predicted values.
We can now calculate how well the model performed by comparing the model's predictions to the true target values, which we reserved in the y_test variable.
First, we'll calculate the confusion matrix to get the necessary parameters:
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, predictions)
TN, FP, FN, TP = confusion_matrix(y_test, predictions).ravel()
print('True Positive(TP) = ', TP)
print('False Positive(FP) = ', FP)
print('True Negative(TN) = ', TN)
print('False Negative(FN) = ', FN)True Positive(TP) = 86
False Positive(FP) = 2
True Negative(TN) = 51
False Negative(FN) = 4With these values, we can now calculate an accuracy score:
accuracy = (TP + TN) / (TP + FP + TN + FN)
print('Accuracy of the binary classifier = {:0.3f}'.format(accuracy))Accuracy of the binary classifier = 0.958Other binary classifiers in the scikit-learn library
Logistic regression is just one of many classification algorithms defined in Scikit-learn. We'll compare several of the most common, but feel free to read more about these algorithms in the sklearn docs here.
We'll also use the sklearn Accuracy, Precision, and Recall metrics for performance evaluation. See the docs here if you'd like to read more about the available metrics.
Initializing each binary classifier
To quickly train each model in a loop, we'll initialize each model and store it by name in a dictionary:
models = {}
# Logistic Regression
from sklearn.linear_model import LogisticRegression
models['Logistic Regression'] = LogisticRegression()
# Support Vector Machines
from sklearn.svm import LinearSVC
models['Support Vector Machines'] = LinearSVC()
# Decision Trees
from sklearn.tree import DecisionTreeClassifier
models['Decision Trees'] = DecisionTreeClassifier()
# Random Forest
from sklearn.ensemble import RandomForestClassifier
models['Random Forest'] = RandomForestClassifier()
# Naive Bayes
from sklearn.naive_bayes import GaussianNB
models['Naive Bayes'] = GaussianNB()
# K-Nearest Neighbors
from sklearn.neighbors import KNeighborsClassifier
models['K-Nearest Neighbor'] = KNeighborsClassifier()Performance evaluation of each binary classifier
Now that we'veinitialized the models, we'll loop over each one, train it by calling .fit(), make predictions, calculate metrics, and store each result in a dictionary.
from sklearn.metrics import accuracy_score, precision_score, recall_score
accuracy, precision, recall = {}, {}, {}
for key in models.keys():
# Fit the classifier
models[key].fit(X_train, y_train)
# Make predictions
predictions = models[key].predict(X_test)
# Calculate metrics
accuracy[key] = accuracy_score(predictions, y_test)
precision[key] = precision_score(predictions, y_test)
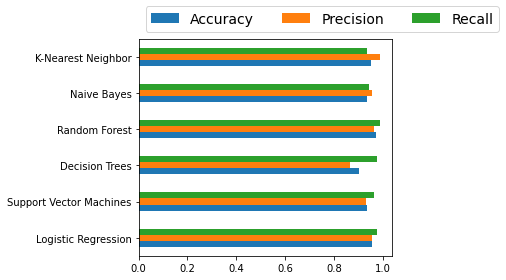
recall[key] = recall_score(predictions, y_test)With all metrics stored, we can use pandas to view the data as a table:
import pandas as pd
df_model = pd.DataFrame(index=models.keys(), columns=['Accuracy', 'Precision', 'Recall'])
df_model['Accuracy'] = accuracy.values()
df_model['Precision'] = precision.values()
df_model['Recall'] = recall.values()
df_model| Accuracy | Precision | Recall | |
|---|---|---|---|
| Logistic Regression | 0.958042 | 0.955556 | 0.977273 |
| Support Vector Machines | 0.937063 | 0.933333 | 0.965517 |
| Decision Trees | 0.902098 | 0.866667 | 0.975000 |
| Random Forest | 0.972028 | 0.966667 | 0.988636 |
| Naive Bayes | 0.937063 | 0.955556 | 0.945055 |
| K-Nearest Neighbor | 0.951049 | 0.988889 | 0.936842 |
Finally, here's a quick bar chart to compare the classifiers' performance:
ax = df_model.plot.barh()
ax.legend(
ncol=len(models.keys()),
bbox_to_anchor=(0, 1),
loc='lower left',
prop={'size': 14}
)
plt.tight_layout()
Since we're only using the default model parameters, we won't know which classifier is better. We should optimize each algorithm's parameters first to know which one has the best performance.
Meet the Authors
Associate Professor of Computer Engineering. Author/co-author of over 30 journal publications. Instructor of graduate/undergraduate courses. Supervisor of Graduate thesis. Consultant to IT Companies.
