Ph.D. in Computer Engineering, Data Scientist
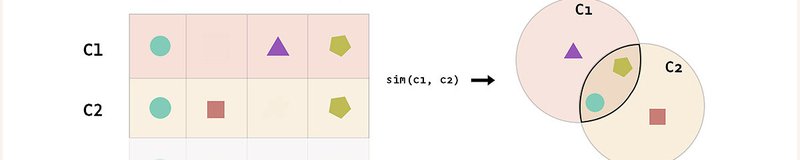
Jaccard Similarity
LearnDataSci is reader-supported. When you purchase through links on our site, earned commissions help support our team of writers, researchers, and designers at no extra cost to you.
You should already know:
Basic Python — Learn Python and Data Science concepts interactively on Dataquest.
What is Jaccard Similarity?
Jaccard Similarity is a common proximity measurement used to compute the similarity between two objects, such as two text documents. Jaccard similarity can be used to find the similarity between two asymmetric binary vectors or to find the similarity between two sets. In literature, Jaccard similarity, symbolized by $J$, can also be referred to as Jaccard Index, Jaccard Coefficient, Jaccard Dissimilarity, and Jaccard Distance.
Jaccard Similarity is frequently used in data science applications. Example use cases for Jaccard Similarity:
- Text mining: find the similarity between two text documents using the number of terms used in both documents
- E-Commerce: from a market database of thousands of customers and millions of items, find similar customers via their purchase history
- Recommendation System: Movie recommendation algorithms employ the Jaccard Coefficient to find similar customers if they rented or rated highly many of the same movies.
1. Jaccard Similarity for Two Binary Vectors
The Jaccard Similarity can be used to compute the similarity between two asymmetric binary variables. Suppose a binary variable has only one of two states: $0$ and $1$, where $0$ means that the attribute is absent, and $1$ means that it is present. While each state is equally valuable for symmetric binary attributes, the two states are not equally important in asymmetric binary variables.
1.1. Numerical Example
Say we are trying to compute the similarity of a store's customers. We could have a binary attribute that corresponds to an item purchased at the store, where $1$ indicates that a specific item was purchased and $0$ indicates that a product was not purchased.
Since there could be thousands of products in the store, the number of products not purchased by any customer is much higher than the number of products purchased. When computing the similarity between customers, we only want to factor in purchases of items. This means that the item purchased is an asymmetric binary variable, making a value of $1$ more important than $0$.
In the first step of a Jaccard Similarity measurement for two customers which consist of $n$ binary attributes, the following four quantities (i.e., frequencies) are computed for the given binary data:
- $a$ = the number of attributes that equal $1$ for both objects $i$ an $j$
- $b$ = the number of attributes that equal $0$ for object $i$ but equal $1$ for object $j$
- $c$ = the number of attributes that equal $1$ for object $i$ but equal $0$ for object $j$
- $d$ = the number of attributes that equal $0$ for both objects $i$ and $j$.
Then, Jaccard Similarity for these attributes is calculated by the following equation:
$$ J(i,j) = sim(i,j) = \frac {a}{a+b+c} $$
Notice the number of $0$ matches is considered unimportant in this computation and is ignored because the items are asymmetric binary attributes.
Suppose that a customer transaction table contains $9$ items and $3$ customers. The similarity between objects is computed based only on the asymmetric attributes.
| item1 | item2 | item2 | item4 | item5 | item6 | item7 | item8 | item9 | |
|---|---|---|---|---|---|---|---|---|---|
| C1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| C2 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| C3 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
The similarity between each pair of the three customers can be calculated by Jaccard Coefficient:
$$J(C1, C2) = \frac {a}{a+b+c} = \frac {1}{1+1+2} = 0.25 \\[20pt] J(C1, C3) = \frac {a}{a+b+c} = \frac {2}{2 + 1 + 1} = 0.5 \\[20pt] J(C2, C3) = \frac {a}{a+b+c} = \frac {0}{0 + 3 + 2} = 0$$
These measurements suggest that $C1$ and $C3$ have similar shopping behavior, whereas $C2$ and $C3$ are not similar since they have purchased completely different items.
Lastly, instead of similarity, the dissimilarity or Jaccard Distance between two binary attributes can be calculated. The dissimilarity based on these attributes by the Jaccard Coefficient is computed as follows:
$$ d(i,j) = \frac {b+c}{a+b+c} \implies 1- sim(i,j) $$
1.2. Python Example
Below, a function is defined to compute Jaccard similarity between two binary vectors. You can also find this builtin to scikit-learn, under sklearn.metrics.jaccard_score.
import numpy as np
def jaccard_binary(x,y):
"""A function for finding the similarity between two binary vectors"""
intersection = np.logical_and(x, y)
union = np.logical_or(x, y)
similarity = intersection.sum() / float(union.sum())
return similarity
# Define some binary vectors
x = [0,1,0,0,0,1,0,0,1]
y = [0,0,1,0,0,0,0,0,1]
z = [1,1,0,0,0,1,0,0,0]
# Find similarity among the vectors
simxy = jaccard_binary(x,y)
simxz = jaccard_binary(x,z)
simyz = jaccard_binary(y,z)
print(' Similarity between x and y is', simxy, '\n Similarity between x and z is ', simxz, '\n Similarity between x and z is ', simyz)
Similarity between x and y is 0.25
Similarity between x and z is 0.5
Similarity between x and z is 0.02. Jaccard Similarity for Two Sets
The Jaccard similarity measures the similarity between two sets of data to see which members are shared and distinct. The Jaccard similarity is calculated by dividing the number of observations in both sets by the number of observations in either set. In other words, the Jaccard similarity can be computed as the size of the intersection divided by the size of the union of two sets. This can be written in set notation using intersection $(A \cap B) $ and unions $(A \cup B)$ of two sets: $$ J(A, B) = \frac {|A \cap B|}{|A \cup B|}$$ where $|A \cap B|$ gives the number of members shared between both sets and $|A \cup B|$ gives the total number of members in both sets (shared and un-shared). The Jaccard Similarity will be $0$ if the two sets don't share any values and $1$ if the two sets are identical. The set may contain either numerical values or strings.
Additionally, this function can be used to find the dissimilarity between two sets by calculating $d(A,B)=1 – J(A,B)$.
2.1. Numerical Example
Example: A simple example is given below to compute the Jaccard similarity between the following two sets.
- $A = \{0,1,2,5,6\}$
- $B = \{0,2,3,4,5,7,9\}$
Jaccard Similarity between two sets is calculated as follows: $$ J(A,B) = \frac {|A∩B|}{|A∪B|} = \frac {|\{0,2,5\}|}{|\{0,1,2,3,4,5,6,7,9\}|} = \frac {3}{9} = 0.33 $$
2.2. Python Example
We can define a function to calculate the Jaccard Similarity between two sets of data in Python like so:
def jaccard_set(list1, list2):
"""Define Jaccard Similarity function for two sets"""
intersection = len(list(set(list1).intersection(list2)))
union = (len(list1) + len(list2)) - intersection
return float(intersection) / union
# Define two sets
a = [0, 1, 2, 5, 6]
b = [0, 2, 3, 4, 5, 7, 9]
# Find Jaccard Similarity between the two sets
jaccard_set(a, b)0.3333333333333333As we can see, the result is identical to the numerical example above. The two sets have a Jaccard Similarity of 0.33.
Meet the Authors
Associate Professor of Computer Engineering. Author/co-author of over 30 journal publications. Instructor of graduate/undergraduate courses. Supervisor of Graduate thesis. Consultant to IT Companies.
Software Developer