The Dot product is a way to multiply two equal-length vectors together. Conceptually, it is the sum of the products of the corresponding elements in the two vectors (see equation below).

Other names for the same operation include:

• Scalar product, because the result produces a single scalar number
• Inner product, reflecting its use with coordinates in Euclidean geometry
• Projection product, because it can be viewed as projecting one vector onto another (see Figure 1)
• The name "dot product" comes from the centered dot " · " used to denote the operation in formulas.

Mathematically, the dot product of two vectors $u = [u_1, u_2, ...u_n]$ and $v=[v_1, v_2... v_n]$ is calculated as:

$$ \begin{align} u \cdot v &= u^T v \\[.5em] \quad \quad &= \sum_{i =1} ^{n} u_iv_i \\[.5em] \quad \quad &= u_1v_1 + u_2v_2 + ...+ u_nv_n \\[.5em] \quad \quad &= \|u\|\|v\| \cos \theta \end{align} $$

In the above equations:

• $u^T$ represents the transpose of the vector $u$.
• $\|u\|$ represents the length (L2 norm) of the vector, meaning the root of the squared elements. $\|u\| = \sqrt{u_1^2 + u_2^2 ... + u_n^2}$
• $\theta$ (theta) is the angle between the vectors.

We use the dot ($\cdot$) symbol to characterize this operation, hence its name. As the alternative "scalar product" name suggests, the result of the operation is a scalar and not a vector, like in the cross product.

The following is an interactive geometric representation of the dot product. Drag the blue and pink vectors to see how the lower right table values change.

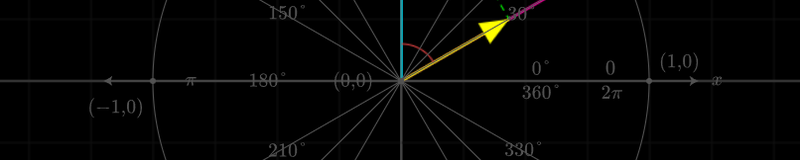
Figure 1: Dot Product Representation

Figure 1 shows the scalar projection of a vector $v$ in the direction of vector $u$. The green line (labeled $v\cos\theta$) is the projection. The scalar product of the vectors is the magnitude of $u$ multiplied by the projection of $v$ on $u$.

When there's a right angle between the two vectors, $\cos90 = 0$, the vectors are orthogonal, and the result of the dot product is 0.

When the angle between two vectors is 0, $\cos0 = 1$, indicating that the vectors are in the same direction (codirectional or parallel). In this case, the dot product is equal to the product of the lengths of the vectors because:

$$ \begin{align} u \cdot v &= \|u\|\|v\|\cos0 \\ &= \|u\|\|v\| \times 1 \\ &= \|u\|\|v\|
\end{align} $$

If the two vectors are normalized—i.e., lengths are equal to 1—the dot product reveals how closely aligned the two vectors are.

For more intuition, see this in-browser applet that lets you experiment with two vectors and their dot product: https://www.falstad.com/dotproduct/

Dot products have the following properties:

• Commutative: $ u \cdot v = v \cdot u $
• Distributive: $ u \cdot (v + y) = u \cdot v + u \cdot y $

The dot product operation is often applied in data science and machine learning. For example:

• cosine similarity is one of the most important similarity metrics and relies on the dot product.
• Neural networks use dot products to compute weighted sums efficiently.
• Calculations of orthogonality

We'll now move on to an example of calculating the dot product numerically.

Suppose that we have the following two-dimentional vectors.

$ u = \begin{bmatrix}5 \\ 12\end{bmatrix}, \quad v = \begin{bmatrix}8 \\ 6 \end{bmatrix}$

Figure 2: Dot Product of two vectors

We can find the dot product by finding the sum of the products of the elements

$$ \begin{align} u \cdot v &= u_1 \times v_1 + u_2 \times v_2 \\ &= 5 \times 8 + 12 \times 6 \\ &= 112 \end{align} $$

Furthermore, we can use this result to find the angle between the vectors using the alternative formula:

$$ \begin{align} \|u\|\|v\| \cos(\theta) &= u \cdot v \\[1em] \|u\|\|v\| \cos(\theta) &= 112 &&\text{From previous result}&\\[1em]
\sqrt{5 \times 5 + 12\times 12} \times \sqrt{8 \times 8 + 6\times 6} \times \cos(\theta) &= 112 \\[1em] 13 \times 10 \times \cos(\theta) &= 112 \\[1em] \cos(\theta) &= 112/130 = 0.8615 \\[1em] \cos(\theta) &= 0.8615 \\[1em] \theta &= \arccos(0.8615) \\[1em] \theta &= 30.5145^{\circ} \end{align} $$

Numpy has the dot() function to calculate the dot product of vectors in Numpy arrays. See this link (https://numpy.org/doc/stable/reference/generated/numpy.dot.html) for details.

The result of the dot product between $u$ and $v$ is 70. The function is computed as: $$ u \cdot v = 1 \times 5 + 2 \times 6 + 3 \times 7 + 4 \times 4 = 70 $$

Alternatively, we can use the shorthand @ operator to calculate dot product (Python 3.5+):

Note that numpy's dot() operation is equivalent to matrix multiplication (numpy matmul() function) for a 2-D array.

Using .dot():

Which is equivalent to:

If you know you're working with matrices, it's better to use matmul() directly to make your code more descriptive.

Completing the following workbook by hand will solidify your understanding of the dot product.