Ph.D. in Computer Engineering, Data Scientist
Benford's Law
Benford’s Law, also called the first digit law, states that the leading digits of numbers in datasets that span large orders of magnitude are distributed in a non-uniform way.
LearnDataSci is reader-supported. When you purchase through links on our site, earned commissions help support our team of writers, researchers, and designers at no extra cost to you.
What is Benford's Law?
Benford’s Law, also called the first digit law, states that the leading digits of numbers in datasets that span large orders of magnitude are distributed in a non-uniform way. Specifically, it shows that the number 1 is observed as the leading digit about 30% — greater than the expected values of 11.1% — and number 9 is observed as the leading digit about 5% — less than the expected values of 11.1 percent (i.e. 1 out of 9). The law provides the probability of leading digits using base-10 logarithms, which results in the expected frequencies of the leading digits to decrease as the digits increase from 1 to 9.
Formula
The probability of the leading digit $d$ ($ d \in {1, ..., 9}$) is estimated with the following logarithmic equation:
$$ P(d) = \log_{10} (d+1) - \log_{10} (d) = \log_{10} (1 + \frac {1}{d}) $$
The equation states that the relative frequency of two consecutive digits ($d$ and $d+1$) is at equal distance on the logarithmic scale. The first digit is not uniformly distributed but fits the logarithmic distribution. The probabilities of the digits calculated by the equation are given below.
| Digit | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Probability | 0.301 | 0.176 | 0.125 | 0.097 | 0.079 | 0.067 | 0.058 | 0.051 | 0.046 |
The real-world data which span multiple orders of magnitude such as stock market prices and populations of countries are more likely to satisfy Benford’s law. For example, the population of countries is spread out on a logarithmic plot over several orders of magnitude rather uniformly. Otherwise, Benford’s law can not be applied accurately to the numbers which spread over one order of magnitude such as heights and age. Because variation in the first digits of the numbers is small.
Use cases
Benford’s law interestingly can be applied to many different real-world data sets. For example, in the 2009 Iranian elections and 2016 Russian Elections, evidence of fraud were observed by applying Benford's Law. The law has also been applied to some presidential elections of the USA to detect electoral fraud. In some examples, data analyst checks the one leading digit as well as two leading digits.
Some real-world examples that are expected to satisfy the law are given below:
- Detecting potential fraud in published data (tax returns, written checks).
- Distribution of the first digits in the population and areas of the countries. Similarly, the population of the counties in the United States satisfies the law.
- Some real-world data such as street numbers, house prices, stock prices, bills
- The first digits of the first 1000 Fibonacci numbers
- The length of the amino acid sequences of some randomly selected proteins.
- The first page of a book is more worn than the others.
- The distance of stars from Earth in light-years
- Twitter users by followers count
- Most common passcodes
These examples clearly show that there are many real-world datasets that satisfy Benford’s Law.
Benford's Law Implementation in Python
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('dark')
Function to compute the probability of a digit using Benford's Law:
def prob_digit(d):
d = int(d)
prob_d = np.log10(1 + 1/d)
return prob_dUsing prob_digit to calculate probabilities of the digits from 1-9:
digits = np.arange(1,10)
digit_probs = np.zeros(len(d))
for digit in digits:
digit_probs[digit - 1] = prob_digit(digit)Plotting the probability results from the previous block:
plt.rc('font', size=16)
fig, ax = plt.subplots(figsize=(12, 6))
ax.bar(digits, digit_probs)
plt.xticks(digits)
plt.xlabel('Digits')
plt.ylabel('Probability')
plt.title("Benford's Law: Probability of Leading Digits")
plt.show()
This plot shows the probability of a leading digit being 1-9 using the Benford's law probability formula. Next we'll see how this maps to a real set of Fibonacci numbers.
Example: Fibonacci Series
The first leading digit of a number is obtained by converting the number to a string and then selecting the first element in the string:
# Calculates and stores the first n = 1000 Fibonacci numbers
def fibonacci(n):
fibs = [1, 1]
for i in range(2, n + 1):
fibs.append(fibs[i - 1] + fibs[i - 2])
return fibs
fib_nums = fibonacci(1000)# Calculate the number of leading digits for 1000 Fibonacci Numbers
def leading_digit_count(numbers):
digit_dict = { 'digit': np.arange(1,10),
'prob' : np.zeros(9),
'count': np.zeros(9) }
for num in numbers:
first_digit = int(str(num)[:1])
ind = np.where(digit_dict['digit'] == first_digit)
digit_dict['count'][ind] = digit_dict['count'][ind] +1
digit_dict['prob'] = digit_dict['count'] / len(numbers)
return digit_dictleading_digit_prob = leading_digit_count(fib_nums)
sse0 = np.sum((leading_digit_prob['prob'] - digit_probs) ** 2)
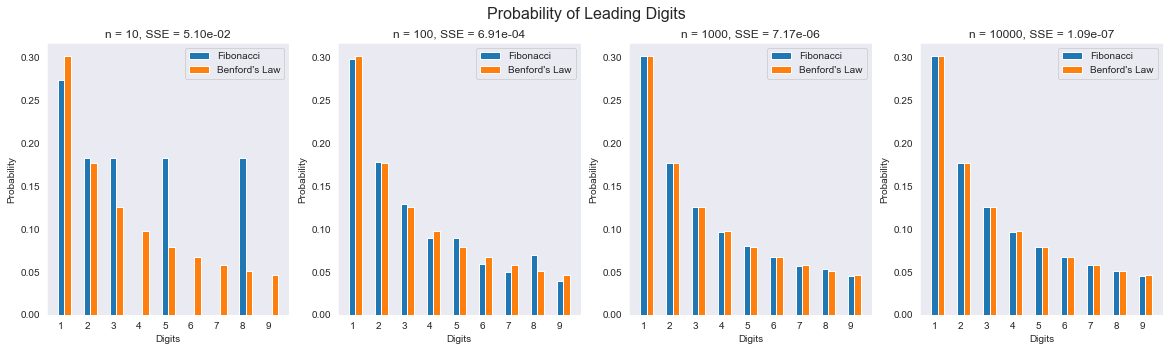
print('Sum of squared errors is ', sse0)Sum of squared errors is 7.17147122318626e-06The sum of squared errors for the probability of leading digits for 1000 Fibonacci numbers very small, showing that these numbers satisfy Benford's law.
Below, we'll plot the first 10, 100, 1,000, and 10,000 Fibonacci numbers against the distribution of numbers according to Benford's Law to show how larger orders of magnitude map closer and closer to Benford's Law
fig, axs = plt.subplots(1, 4, figsize=(20,5))
for i, ax in enumerate(axs):
n = 10 ** (i + 1)
fib_nums = fibonacci(n)
leading_digit_prob = leading_digit_count(fib_nums)
sse0 = np.sum((leading_digit_prob['prob'] - digit_probs) ** 2)
ax.bar(leading_digit_prob['digit'], leading_digit_prob['prob'], width=0.25)
ax.bar(digits + 0.25, digit_probs, width = 0.25)
ax.set_xticks(leading_digit_prob['digit'])
ax.set_xlabel('Digits')
ax.set_ylabel('Probability')
ax.set_title(f'n = {n}, SSE = {sse0:.2e}')
ax.legend(labels=['Fibonacci', "Benford's Law"])
plt.suptitle(f'Probability of Leading Digits', fontsize=16)
plt.show()
As you can see, as the size of the set of Fibonacci numbers grow, the error between Benford's Law and the leading digit of the Fibonacci numbers gets smaller and smaller.
Meet the Authors
Associate Professor of Computer Engineering. Author/co-author of over 30 journal publications. Instructor of graduate/undergraduate courses. Supervisor of Graduate thesis. Consultant to IT Companies.